Назад | Содержание | Вперёд
Списки можно применять для представления множеств, хотя и существует некоторое различие между этими понятиями: порядок элементов множества не существенен, в то время как для списка этот порядок имеет значение; кроме того, один н тот же объект может встретиться в списке несколько раз. Однако наиболее часто используемые операции над списками аналогичны операциям над множествами. Среди них
В оставшейся части раздела мы покажем программы, реализующие эти и некоторые другие операции над списками.
Мы представим отношение принадлежности как
принадлежит( X, L)
где Х - объект, а L - список. Цель принадлежит( X, L) истинна, если элемент Х встречается в L. Например, верно что
принадлежит( b, [а, b, с] )
и, наоборот, не верно, что
принадлежит b, [а, [b, с] ] )
но
принадлежит [b, с], [а, [b, с]] )
истинно. Составление программы для отношения принадлежности может быть основано на следующих соображениях:
(1) Х есть голова L, либо
(2) Х принадлежит хвосту L.
Это можно записать в виде двух предложений, первое из которых есть простой факт, а второе - правило:
принадлежит( X, [X | Хвост ] ).
принадлежит ( X,
[Голова | Хвост ] ) :-
принадлежит( X, Хвост).
Для сцепления списков мы определим отношение
конк( L1, L2, L3)
Здесь L1 и L2 - два списка, a L3 - список, получаемый при их сцеплении. Например,
конк( [а, b], [c, d], [a, b, c, d] )
истинно, а
конк( [а, b], [c, d], [a, b, a, c, d] )
ложно. Определение отношения конк, как и раньше, содержит два случая в зависимости от вида первого аргумента L1:
(1) Если первый аргумент пуст, тогда второй и третий аргументы представляют собой один и тот же список (назовем его L), что выражается в виде следующего прологовского факта:
конк( [ ], L, L ).
(2) Если первый аргумент отношения конк не пуст, то он имеет голову и хвост в выглядит так:
[X | L1]
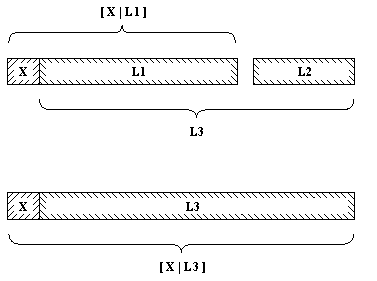
На рис. 3.2 показано, как производится сцепление списка [X | L1] с произвольным списком L2. Результат сцепления - список [X | L3], где L3 получен после сцепления списков L1 и L2. На прологе это можно записать следующим образом:
конк( [X | L1, L2, [X | L3]):-
конк(
L1, L2, L3).

Рис. 3. 2. Конкатенация списков.
Составленную программу можно теперь использовать для сцепления заданных списков, например:
?- конк( [a, b, с], [1, 2, 3],
L ).
L = [a, b, c, 1, 2, 3]
?- конк( [а, [b, с], d], [а,
[ ], b], L ).
L = [a, [b, c], d, а, [ ], b]
Хотя программа для конк выглядит довольно просто, она обладает большой гибкостью и ее можно использовать многими другими способами. Например, ее можно применять как бы в обратном направлении для разбиения заданного списка на две части:
?- конк( L1, L2, [а, b, с] ).
L1 = [ ]
L2 = [а, b, c];
L1 = [а]
L2 = [b, с];
L1 = [а, b]
L2 = [c];
L1 = [а, b, с]
L2 = [ ];
no (нет)
Список [а, b, с] разбивается на два списка четырьмя способами, и все они были обнаружены нашей программой при помощи механизма автоматического перебора.
Нашу программу можно также применить для поиска в списке комбинации элементов, отвечающей некоторому условию, задаваемому в виде шаблона или образца. Например, можно найти все месяцы, предшествующие данному, и все месяцы, следующие за ним, сформулировав такую цель:
?- конк( До, [май |
После ],
[янв, фев, март, апр, май, июнь,
июль, авг, сент, окт, ноябрь, дек]).
До = [янв, фев, март, апр]
После = [июнь, июль, авг, сент, окт, ноябрь, дек].
Далее мы сможем найти месяц, непосредственно предшествующий маю, и месяц, непосредственно следующий за ним, задав вопрос:
?- конк( _, [Месяц1,
май, Месяц2 | _ ],
[янв, февр, март, апр, май, июнь,
июль, авг, сент, окт, ноябрь, дек]).
Месяц1 = апр
Месяц2 = июнь
Более того, мы сможем, например, удалить из некоторого списка L1 все, что следует за тремя последовательными вхождениями элемента z в L1 вместе с этими тремя z. Например, это можно сделать так:
?- L1 = [a, b, z, z, c, z, z, z, d,
e],
конк( L2, [z, z, z
| _ ], L1).
L1 = [a, b, z, z, c, z, z, z, d, e]
L2 = [a, b, z, z, c]
Мы уже запрограммировали отношение принадлежности. Однако, используя конк, можно было бы определить это отношение следующим эквивалентным способом:
принадлежит1( X, L) :-
конк( L1, [X | L2], L).
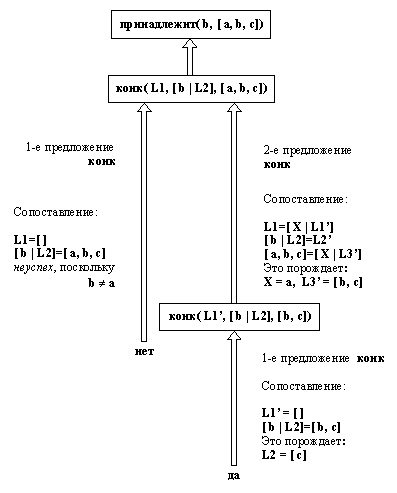
Рис. 3. 3. Процедура принадлежит1
находит элемент в заданном
списке, производя по нему последовательный
поиск.
В этом предложении сказано: "X принадлежит L, если список L можно разбить на два списка таким образом, чтобы элемент Х являлся головой второго из них. Разумеется, принадлежит1 определяет то же самое отношение, что и принадлежит. Мы использовали другое имя только для того, чтобы различать таким образом две разные реализации этого отношения, Заметим, что, используя анонимную переменную, можно записать вышеприведенное предложение так:
принадлежит1( X, L) :-
конк( _, [X | _ ], L).
Интересно сравнить между собой эти две реализации отношения принадлежности. Принадлежит имеет довольно очевидный процедурный смысл:
Для проверки, является ли Х элементом списка L, нужно
(1) сначала проверить, не совпадает ли голова списка L с X, а затем
(2) проверить, не принадлежит ли Х хвосту списка L.
С другой стороны, принадлежит1, наоборот, имеет очевидный декларативный смысл, но его процедурный смысл не столь очевиден.
Интересным упражнением было бы следующее: выяснить, как в действительности принадлежит1 что-либо вычисляет. Некоторое представление об этом мы получим, рассмотрев запись всех шагов вычисления ответа на вопрос:
?- принадлежит1( b, [а, b, с] ).
На рис. 3.3 приведена эта запись. Из нее можно заключить, что принадлежит1 ведет себя точно так же, как и принадлежит. Он просматривает список элемент за элементом до тех пор, пока не найдет нужный или пока не кончится список.
3. 1. (а) Используя отношение конк, напишите цель, соответствующую вычеркиванию трех последних элементов списка L, результат - новый список L1. Указание: L - конкатенация L1 и трехэлементного списка.
(b) Напишите последовательность целей для порождения списка L2, получающегося из списка L вычеркиванием его трех первых и трех последних элементов.
3. 2. Определите отношение
последний( Элемент, Список)
так, чтобы Элемент являлся последним элементом списка Список. Напишите два варианта определения: (а) с использованием отношения конк, (b) без использования этого отношения.
Наиболее простой способ добавить элемент в список - это вставить его в самое начало так, чтобы он стал его новой головой. Если Х - это новый элемент, а список, в который Х добавляется - L, тогда результирующий список - это просто
[X | L]
Таким образом, для того, чтобы добавить новый элемент в начало списка, не надо использовать никакой процедуры. Тем не менее, если мы хотим определить такую процедуру в явном виде, то ее можно представить в форме такого факта:
добавить( X, L, [X | L] ).
Удаление элемента Х из списка L можно запрограммировать в виде отношения
удалить( X, L, L1)
где L1 совпадает со списком L, у которого удален элемент X. Отношение удалить можно определить аналогично отношению принадлежности. Имеем снова два случая:
(1) Если Х является головой списка, тогда результатом удаления будет хвост этого списка.
(2) Если Х находится в хвосте списка, тогда его нужно удалить оттуда.
удалить( X, [X | Хвост], Хвост).
удалить( X, [Y | Хвост],
[ Y | Хвост1] ) :-
удалить( X, Хвост, Хвост1).
как и принадлежит, отношение удалить по природе своей недетерминировано. Если в списке встречается несколько вхождений элемента X, то удалить сможет исключить их все при помощи возвратов. Конечно, вычисление по каждой альтернативе будет удалять лишь одно вхождение X, оставляя остальные в неприкосновенности. Например:
?- удалить( а, [а, b, а, а], L].
L = [b, а, а];
L = [а, b, а];
L = [а, b, а];
nо (нет)
При попытке исключить элемент, не содержащийся в списке, отношение удалить потерпит неудачу.
Отношение удалить можно использовать в обратном направлении для того, чтобы добавлять элементы в список, вставляя их в произвольные места. Например, если мы хотим во все возможные места списка [1, 2, 3] вставить атом а, то мы можем это сделать, задав вопрос: "Каким должен быть список L, чтобы после удаления из него элемента а получился список [1, 2, 3]?"
?- удалить( а, L, [1, 2, 3] ).
L = [а, 1, 2, 3];
L = [1, а, 2, 3];
L = [1, 2, а, 3];
L = [1, 2, 3, а];
nо (нет)
Вообще операция по внесению Х в произвольное место некоторого списка Список, дающее в результате БольшийСписок, может быть определена предложением:
внести( X, Список,
БольшийСписок) :-
удалить( X, БольшийСписок, Список).
В принадлежит1 мы изящно реализовали отношение принадлежности через конк. Для проверки на принадлежность можно также использовать и удалить. Идея простая: некоторый Х принадлежит списку Список, если Х можно из него удалить:
принадлежит2( X,
Список) :-
удалить( X, Список, _ ).
Рассмотрим теперь отношение подсписок. Это отношение имеет два аргумента - список L и список S, такой, что S содержится в L в качестве подсписка. Так отношение
подсписок( [c, d, e], [a, b, c, d, e, f] )
имеет место, а отношение
подсписок( [c, e], [a, b, c, d, e, f] )
нет. Пролог-программа для отношения подсписок может основываться на той же идее, что и принадлежит1, только на этот раз отношение более общо (см. рис. 3.4).
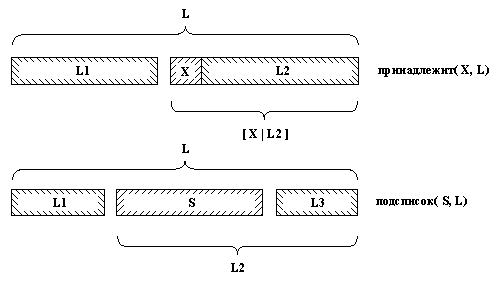
Рис. 3. 4. Отношения принадлежит и подсписок.
Его можно сформулировать так:
S является подсписком L, если
(1) L можно разбить на два списка L1 и L2 и
(2) L2 можно разбить на два списка S и L3.
Как мы видели раньше, отношение конк можно использовать для разбиения списков. Поэтому вышеприведенную формулировку можно выразить на Прологе так:
подсписок( S, L) :-
конк( L1, L2, L),
конк( S, L3, L2).
Ясно, что процедуру подсписок можно гибко использовать различными способами. Хотя она предназначалась для проверки, является ли какой-либо список подсписком другого, ее можно использовать, например, для нахождения всех подсписков данного списка:
?- подсписок( S, [а, b, с] ).
S = [ ];
S = [a];
S = [а, b];
S = [а, b, с];
S = [b];
. . .
Иногда бывает полезно построить все перестановки некоторого заданного списка. Для этого мы определим отношение перестановка с двумя аргументами. Аргументы - это два списка, один из которых является перестановкой другого. Мы намереваемся порождать перестановки списка с помощью механизма автоматического перебора, используя процедуру перестановка, подобно тому, как это делается в следующем примере:
?- перестановка( [а, b, с], Р).
Р = [а, b, с];
Р = [а, с, b];
Р = [b, а, с];
. . .
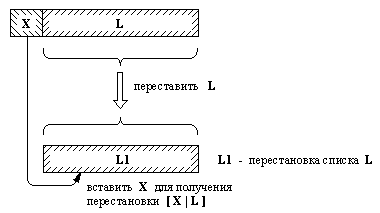
Рис. 3. 5. Один из способов построения перестановки списка [X | L].
Программа для отношения перестановка в свою очередь опять может основываться на рассмотрении двух случаев в зависимости от вида первого списка:
(1) Если первый список пуст, то и второй список должен быть пустым.
(2) Если первый список не пуст, тогда он имеет вид [Х | L], и перестановку такого списка можно построить так, как Это показано на рис. 3.5: вначале получить список L1 - перестановку L, а затем внести Х в произвольную позицию L1.
Два прологовских предложения, соответствующих этим двум случаям, таковы:
перестановка( [ ], [ ]).
перестановка( [X | L ],
Р) :-
перестановка( L, L1),
внести( X, L1, Р).
Другой вариант этой программы мог бы предусматривать удаление элемента Х из первого списка, перестановку оставшейся его части - получение списка Р, а затем добавление Х в начало списка Р. Соответствующая программа такова:
перестановка2( [ ], [ ]).
перестановка2( L, [X |
Р] ) :-
удалить( X, L, L1),
перестановка2( L1, Р).
Поучительно проделать несколько экспериментов с нашей программой перестановки. Ее нормальное использование могло бы быть примерно таким:
?- перестановка( [красный, голубой, зеленый], Р).
Как и предполагалось, будут построены все шесть перестановок:
Р = [ красный,
голубой, зеленый];
Р = [ красный, зеленый,
голубой];
Р = [ голубой, красный,
зеленый];
Р = [ голубой, зеленый,
красный];
Р = [ зеленый, красный,
голубой];
Р = [ зеленый, голубой,
красный];
nо (нет)
Приведем другой вариант использования процедуры перестановка:
?- перестановка( L, [а, b, с] ).
Наша первая версия, перестановка, произведет успешную конкретизацию L всеми шестью перестановками. Если пользователь потребует новых решений, он никогда не получит ответ "нет", поскольку программа войдет в бесконечный цикл, пытаясь отыскать новые несуществующие перестановки. Вторая версия, перестановка2, в этой ситуации найдет только первую (идентичную) перестановку, а затем сразу зациклится. Следовательно, при использовании этих отношений требуется соблюдать осторожность.
3. 3. Определите два предиката
четнаядлина( Список) и нечетнаядлина( Список)
таким образом, чтобы они были истинными, если их аргументом является список четной или нечетной длины соответственно. Например, список [а, b, с, d] имеет четную длину, a [a, b, c] - нечетную.
3. 4. Определите отношение
обращение( Список, ОбращенныйСписок),
которое обращает списки. Например,
обращение( [a, b, c, d], [d, c, b, a] ).
3. 5. Определите предикат
палиндром( Список).
Список называется палиндромом, если он читается одинаково, как слева направо, так и справа налево. Например, [м, а, д, а, м].
3. 6. Определите отношение
сдвиг( Список1, Список2)
таким образом, чтобы Список2 представлял собой Список1, "циклически сдвинутый" влево на один символ. Например,
?- сдвиг( [1, 2, 3, 4,
5], L1),
сдвиг1( LI,
L2)
дает
L1 = [2, 3, 4, 5, 1]
L2 = [3, 4, 5, 1, 2]
3. 7. Определите отношение
перевод( Список1, Список2)
для перевода списка чисел от 0 до 9 в список соответствующих слов. Например,
перевод( [3, 5, 1, 3], [три, пять, один, три] )
Используйте в качестве вспомогательных следующие отношения:
означает( 0, нуль).
означает( 1, один).
означает( 2, два).
. . .
3. 8. Определите отношение
подмножество( Множество, Подмножество)
где Множество и Подмножество - два списка представляющие два множества. Желательно иметь возможность использовать это отношение не только для проверки включения одного множества в другое, но и для порождения всех возможных подмножеств заданного множества. Например:
?- подмножество( [а, b, с], S ).
S = [a, b, c];
S = [b, c];
S = [c];
S = [ ];
S = [a, c];
S = [a];
. . .
3. 9. Определите отношение
разбиениесписка( Список, Список1, Список2)
так, чтобы оно распределяло элементы списка между двумя списками Список1 и Список2 и чтобы эти списки были примерно одинаковой длины. Например:
разбиениесписка( [а, b, с, d, e], [a, с, е], [b, d]).
3. 10. Перепишите программу об обезьяне и бананах из главы 2 таким образом, чтобы отношение
можетзавладеть( Состояние, Действия)
давало не только положительный или отрицательный ответ, но и порождало последовательность действий обезьяны, приводящую ее к успеху. Пусть Действия будет такой последовательностью, представленной в виде списка ходов:
Действия = [ перейти(
дверь, окно),
передвинуть( окно, середина),
залезть, схватить ]
3. 11. Определите отношение
линеаризация( Список, ЛинейныйСписок)
где Список может быть списком списков, а ЛинейныйСписок - это тот же список, но "выровненный" таким образом, что элементы его подсписков составляют один линейный список. Например:
? - линеаризация( [а, d, [с, d], [ ], [[[е]]], f, L).
L = [a, b, c, d, e, f]
Назад | Содержание | Вперёд