Назад | Содержание | Вперёд
При реализации какой-либо игровой программы на языке AL0 ее можно для удобства разбить на три модуля:
(1)
интерпретатор языка AL0,
(2) таблица
советов на языке AL0,
(3) библиотека
предикатов, используемых в таблице советов (в том
числе
предикаты, задающие правила игры).
Эта структура соответствует обычной структуре системы, основанной на знаниях:
Реализация на Прологе миниатюрного, не зависящего от конкретной игры интерпретатора языка AL0 показана на рис. 15.6. Эта программа осуществляет также взаимодействие с пользователем во время игры. Центральная задача этой программы - использовать знания, записанные в таблице советов, то есть интерпретировать программу на языке советов AL0 с целью построения форсированных деревьев и их "исполнения" в процессе игры. Базовый алгоритм порождения форсированных деревьев аналогичен поиску с предпочтением в И / ИЛИ-графах гл. 13, при этом форсированное дерево соответствует решающему И / ИЛИ-дереву. Этот алгоритм также напоминает алгоритм построения решающего дерева ответа на вопрос пользователя, применявшийся в оболочке экспертной системы (гл. 14).
Программа на рис. 15.6 составлена в предположении, что она играет белыми, а ее противник - черными. Программа запускается процедурой
% Миниатюрный интерпретатор языка
AL0
%
% Эта программа играет, начиная с заданной
позиции,
% используя знания, записанные на языке AL0
:- ор( 200, xfy, :).
:- ор( 220, xfy, ..).
:- ор( 185, fx, если).
:- ор( 190, xfx, то).
:- ор( 180, xfy, или).
:- ор( 160, xfy, и).
:- ор( 140, fx, не).
игра( Поз) :-
% Играть, начиная с Поз
игра( Поз, nil).
% Начать с пустого
форсированного дерева
игра( Поз, ФорсДер) :-
отобр( Поз),
( конец_игры( Поз),
% Конец игры?
write( 'Конец игры'), nl, !;
сделать_ход( Поз, ФорсДер, Поз1, ФорсДер1), !,
игра( Поз1, ФорсДер1) ).
% Игрок ходит в соответствии с форсированным деревом
сделать_ход( Поз,
Ход .. ФДер1, Поз1, ФДер1) :-
чей_ход(
Поз, б),
% Программа играет белыми
разрход( Поз, Ход, Поз1),
показать_ход( Ход).
% Прием хода противника
сделать_ход( Поз,
ФДер, Поз1, ФДер1) :-
чей_ход( Поз, ч),
write( 'Ваш ход:'),
read( Ход),
( разрход( Поз, Ход, Поз1),
поддер( ФДер, Ход, ФДер1), !;
% Вниз по форс. дереву
write( 'Неразрешенный ход'), nl,
сделать_ход( Поз, ФДер, Поз1, ФДер1) ).
% Если текущее форсированное дерево пусто, построить новое
сделать_ход( Поз, nil,
Поз1, ФДер1) :-
чей_ход( Поз, б),
восст_глуб( Поз, Поз0),
% Поз0 = Поз с глубиной 0
стратегия( Поз0, ФДер), !,
% Новое форсированное дерево
сделать_ход( Поз0, ФДер, Поз1, ФДер1).
% Выбрать форсированное поддерево, соответствующее Ход' у
поддер( ФДеревья,
Ход, Фдер) :-
принадлежит( Ход . . Фдер, ФДеревья), !.
поддер( _, _, nil).
стратегия( Поз,
ФорсДер) :-
% Найти форс. дерево для Поз
Прав : если Условие то СписСов,
% Обращение к таблице советов
удовл( Условие, Поз, _ ), !,
% Сопоставить Поз с предварительным условием
принадлежит( ИмяСовета, СписСов),
% По очереди попробовать элем. советы
nl, write( 'Пробую'), write( ИмяСовета),
выполн_совет( ИмяСовета, Поз, ФорсДер), !.
выполн_совет(
ИмяСовета, Поз, Фдер) :-
совет( ИмяСовета, Совет),
% Найти элементарный совет
выполн( Совет, Поз, Поз, ФДер).
% "выполн" требует две позиции для
сравнивающих предикатов
выполн( Совет, Поз,
КорнПоз, ФДер) :-
поддержка( Совет, ЦП),
удовл( ЦП, Поз, КорнПоз),
%
Сопоставить Поз с целью-поддержкой
выполн1( Совет, Поз, КорнПоз, ФДер).
выполн1( Совет, Поз,
КорнПоз, nil) :-
главцель( Совет, ГлЦ),
удовл( ГлЦ, Поз, КорнПоз), !.
%
Главная цель удовлетворяется
выполн1( Совет, Поз,
КорнПоз, Ход .. ФДеревья) :-
чей_ход( Поз, б), !,
%
Программа играет белыми
ходы_игрока( Совет, ХодыИгрока),
%
Ограничения на ходы игрока
ход( ХодыИгрока, Поз, Ход, Поз1),
%
Ход, удовлетворяющий ограничению
выполн( Совет, Поз1, КорнПоз, ФДеревья).
выполн1( Совет, Поз,
КорнПоз, ФДеревья) :-
чей_ход( Поз, ч), !,
% Противник
играет черными
ходы_противника( Совет, ХодыПр),
bagof ( Ход . . Поз1, ход( ХодыПр, Поз, Ход, Поз1), ХПспис),
выполн_все( Совет, ХПспис, КорнПоз, ФДеревья).
%
Совет выполним во всех преемниках Поз
выполн_все( _, [ ], _, [ ]).
выполн_все( Совет,
[Ход . . Поз | ХПспис], КорнПоз,
[Ход . . ФД | ФДД] ) :-
выполн( Совет, Поз, КорнПоз, ФД),
выполн_все( Совет, ХПспис, КорнПоз, ФДД).
% Интерпретация главной цели и
цели-поддержки:
% цель - это И / ИЛИ / НЕ комбинация. имен предикатов
удовл( Цель1 и Цель2,
Поз, КорнПоз) :- !,
удовл( Цель1, Поз, КорнПоз),
удовл( Цель2, Поз, КорнПоз).
удовл( Цель1 или
Цель2, Поз, КорнПоз) :- !,
( удовл( Цель1, Поз, КорнПоз);
удовл( Цель2, Поз, КорнПоз) ).
удовл( не Цель, Поз,
КорнПоз) :- !,
not удовл( Цель, Поз, КорнПоз ).
удовл( Пред, Поз,
КорнПоз) :-
( Усл =.. [Пред, Поз];
% Большинство предикатов не зависит от КорнПоз
Усл =.. [Пред, Поз, КорнПоз] ),
call( Усл).
% Интерпретация ограничений на ходы
ход( Ходы1 и Ходы2,
Поз, Ход, Поз1) :- !,
ход( Ходы1, Поз, Ход, Поз1),
ход( Ходы2, Поз, Ход, Поз1).
ход( Ходы1 затем
Ходы2, Поз, Ход, Поз1) :- !,
( ход( Ходы1, Поз, Ход, Поз1);
ход( Ходы2, Поз, Ход, Поз1) ).
% Доступ к компонентам элементарного совета
главцель( ГлЦ : _, ГлЦ).
поддержка( ГлЦ : ЦП : _, ЦП).
ходы_игрока( ГлЦ : ЦП : ХодыИгрока : _, Ходы Игрока).
ходы_противника(
ГлЦ : ЦП: ХодыИгр : ХодыПр :_,
ХодыПр).
принадлежит( X, [X | Спис]).
принадлежит( X, [Y |
Спис]) :-
принадлежит( X, Спис).
Рис. 15. 6. Миниатюрный интерпретатор языка AL0.
игра( Поз)
где Поз - выбранная начальная позиция. Если в позиции Поз ходит противник, то программа принимает его ход, в противном случае - "консультируется" с таблицей советов, приложенной к программе, порождает форсированное дерево и делает свой ход в соответствии с этим деревом. Так продолжается до окончания игры, которое обнаруживает предикат конец_игры (например, если поставлен мат).
Форсированное дерево - это дерево ходов, представленное в программе следующей структурой:
Ход . . [ Ответ1 . . Фдер1, Ответ2 . . Фдер2, . . . ]
Здесь ".." - инфиксный оператор; Ход - первый ход "игрока"; Ответ1, Ответ2, ... - возможные ответы противника; Фдер1, Фдер2, ... - форсированные поддеревья для каждого из этих ответов
.Общий принцип достижения выигрыша королем и ладьей против единственной фигуры противника, короля, состоит в том, чтобы заставить короля отступить к краю доски или, при необходимости, загнать его в угол, а затем поставить мат в несколько ходов. В детальном изложении эта стратегия выглядит так:
Повторять циклически, пока не будет поставлен мат (постоянно проверяя, что не возникла патовая позиция и что нет нападения на незащищенную ладью):
(1) Найти способ поставить королю противника мат в два хода.
(2) Если не
удалось, то найти способ уменьшить ту область
доски, в которой
король противника "заперт" под воздействием
ладьи.
(3) Если и это
не удалось, то найти способ приблизить своего
короля к королю
противника.
(4) Если ни один
из элементарных советов 1, 2, или 3 не выполним, то
найти
способ сохранить все имеющиеся к настоящему
моменту "достижения" в
смысле (2) и (3) (т. е. сделать выжидающий ход).
(5) Если ни одна
из целей 1, 2, 3 или 4 не достижима, то найти способ
получить
позицию, в которой ладья занимает вертикальную
или горизонтальную
линию, отделяющую одного короля от другого.
Описанные выше принципы реализованы во всех деталях в таблице советов на языке AL0, показанной на рис. 15.7. Эта таблица может работать под управлением интерпретатора рис. 15.6. Рис. 15.8 иллюстрирует смысл некоторых из предикатов, использованных в таблице советов, а также показывает, как эта таблица работает.
В таблице используются следующие предикаты:
Предикаты целей
мат мат королю противника
пат пат королю противника
потеря_ладьи король противника может взять ладью
ладья_под_боем
король противника
может напасть на ладью прежде, чем наш
король сможет ее защитить
уменьш_простр
уменьшилось
"жизненное пространство" короля противника,
ограничиваемое ладьей
раздел
ладья
занимает вертикальную или горизонтальную линию,
разделяющую королей
ближе_к_клетке
наш король приблизился к "критической
клетке" (см. рис. 15.9),
т.е. манхеттеновское расстояние до нее
уменьшилось
l_конфиг "L-конфигурация" (рис. 15.9)
простр_больше_2
"жизненное пространство" короля противника
занимает
больше двух клеток
Предикаты, ограничивающие ходы
глубина = N
ход на глубине N дерева поиска
разреш
любой разрешенный ход
ход_шах
ход, объявляющий шах
ход_ладьей
ход ладьей
нет_хода
ни один ход не подходит
сначала_диаг
ход
королем, преимущественно по диагонали
% Окончание "король и ладья против короля" на языке AL0
% Правила
правило_края:
если король_противника_на_краю и
короли_рядом
то [мат_2, потеснить, приблизиться,
сохранить_простр, отделить_2,
отделить_3].
иначе_правило
если любая_поз
то [ потеснить, приблизиться,
сохранить_простр,
отделить_2, отделить_3].
% Элементарные советы
совет( мат_2,
мат :
не потеря_ладьи и
король_противника_на_краю:
(глубина = 0) и разреш
затем (глубина = 2) и ход_шах :
(глубина = 1) и разреш ).
совет( потеснить,
уменьш_простр и не ладья_под_боем и
раздел и не пат :
не потеря_ладьи :
(глубина = 0) и ход_ладьей :
нет_хода ).
совет(
приблизиться,
ближе _к_клетке и не ладья_под_боем и
(раздел или l_конфиг) и
(простр_больше_2 или не
наш_король_на_краю):
не потеря_ладьи :
(глубина = 0) и сначала_диаг :
нет_хода ).
совет(
сохранить_простр,
ход_противиика и не ладья_под_боем и
раздел
и не_дальше_от_ладьи и
(простр_больше_2 или не
наш_король_на_краю):
не потеря_ладьи :
(глубина = 0) и сначала_диаг :
нет_хода ).
совет( отделить_2,
ход_противника и раздел и не
ладья_под_боем:
не потеря_ладьи :
(глубина < 3) и разреш :
(глубина < 2) и разреш ).
совет( отделить_3,
ход_противника и раздел и не
ладья_под_боем:
не потеря_ладьи :
(глубина < 5) и разреш :
(глубина < 4) и разреш ).
Рис. 15. 7. Таблица
советов на языке AL0 для окончания "король
и ладья против короля". Таблица состоит из двух
правил и шести
элементарных советов.

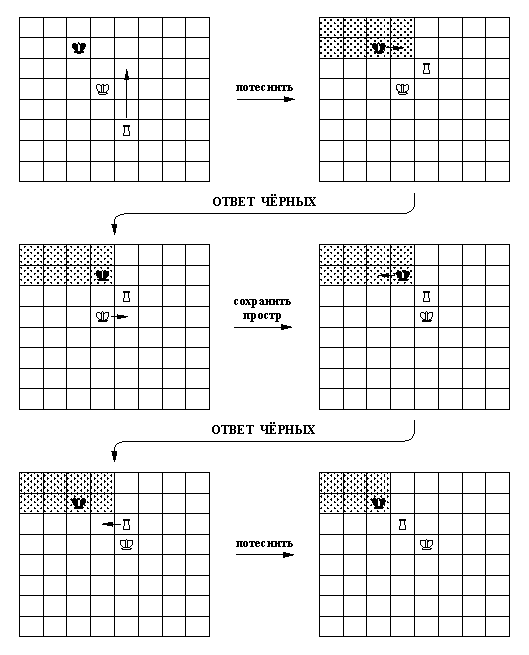
Рис. 15. 8. Фрагмент
шахматной партии, полученный с использованием
таблицы советов рис. 15.7 и иллюстрирующий
применение стратегии
оттеснения короля в угол доски. В этой
последовательности ходов
выполнялись элементарные советы: сохранить_
простр (выжидающий
ход, сохраняющий "жизненное
пространство" черного короля) и
потеснить (ход, сокращающий
"жизненное пространство"). Область,
в которой заключен черный король, выделена
штриховкой. После
выполнения последнего совета потеснить
эта область сократилась
с восьми до шести клеток.
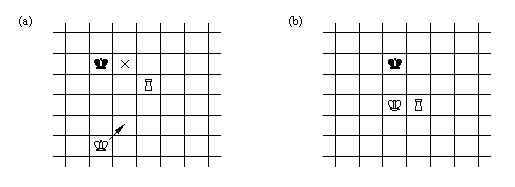
Рис. 15. 9. (а)
"Критическая клетка" отмечена крестиком.
Она
используется при маневрировании с целью
оттеснить черного
короля. Белый король приближается к
"критической клетке",
двигаясь, как указано на рисунке. (б)
Три фигуры образуют
конфигурацию, напоминающую букву L.
Аргументами этих предикатов являются либо позиции (в предикатах целей), либо ходы (в предикатах, ограничивающих ходы). Предикаты целей могут иметь один или два аргумента. Первый из аргументов - это всегда текущая вершина поиска; второй аргумент (если он имеется) - корневая вершина дерева поиска. Второй аргумент необходим в так называемых сравнивающих предикатах, которые сравнивают корневую и текущую позиции в том или ином отношении. Например, предикат уменьш_простр проверяет, сократилось ли "жизненное пространство" короля противника (рис. 15.8). Эти предикаты вместе с шахматными правилами (применительно к окончанию "король и ладья против короля"), а также процедура для отображения текущего состояния игровой доски ( отобр ( Поз) ) запрограммированы на рис. 15.10.
На рис. 15.8 показано, как играет наша программа, основанная на механизме советов. При продолжении игры из последней позиции рис. 15.8 она могла бы протекать так, как в приведенном ниже варианте (в предположении, что "противник" ходит именно так, как указано). Здесь использована алгебраическая шахматная нотация, в которой вертикальные линии пронумерованы, как 'а', 'b', 'с', .... а горизонтальные - как 1, 2, 3, ... . Например, ход ЧК b7 означает: передвинуть черного короля на клетку. расположенную на пересечении вертикальной линии 'b' с горизонтальной линией 7.
...
ЧК b7
БК d5
ЧК с7
БК с5
ЧК b7
БЛ с6
ЧК а7
БЛ b6
ЧК а8
БК b5
ЧК а7
БК с6
ЧК а8
БК с7
ЧК а7
БЛ с6
ЧК а8
БЛ а6
мат
Теперь уместно задать некоторые вопросы. Во-первых, является ли наша программа-советчик корректной в том смысле, что она ставит мат при любом варианте защиты со стороны противника и при любой начальной позиции, в которой на доске король и ладья против короля? В статье Bratko (1978) приведено формальное доказательство того, что таблица советов, практически совпадающая с таблицей рис. 15.7, действительно является корректной в указанном смысле.
Другой возможный вопрос: является ли программа оптимальной, то есть верно ли, что она ставит мат за минимальное число ходов? Нетрудно показать на примерах, что игру нашей программы в этом смысле нельзя назвать оптимальной. Известно, что оптимальный вариант в этом окончании (т.е. предполагающий оптимальную игру с обеих сторон) имеет длину не более 16 ходов. Хотя наша таблица советов и далека от этого оптимума, было показано, что число, ходов наверняка не превосходит 50. Это важный результат в связи с тем, что в шахматах существует "правило 50-ти ходов": в эндшпилях типа "король и ладья против короля" противник, имеющий преимущество, должен поставить, мат не более, чем за 50 ходов; иначе может быть объявлена ничья.
Рассмотрите какой-нибудь другой простой эндшпиль, например "король и пешка против короля", и напишите для него программу на языке AL0 (вместе с определениями соответствующих предикатов).
% Библиотека предикатов для окончания
% "король и ладья против короля"
% Позиция представлена стуктурой:
% ЧейХод..Бх : Бу..Лх : Лу..Чх : Чу..Глуб
% ЧейХод - с чьей стороны ход в этой позиции ('б' или
'ч')
% Бх, Бу - координаты белого короля
% Лх, Лу - координаты белой ладьи
% Чх, Чу - координаты черного короля
% Глуб - глубина, на которой находится эта позиция
в дереве
% поиска
% Отношения выбора элементов позиции
чей_ход( ЧейХод.._,
ЧейХод).
бк( _..БК.._, БК).
% Белый король
бл( _.._..БЛ.._, БЛ).
% Белая ладья
чк( _.._.._..ЧК.._, ЧК).
% Черный король
глуб( _.._.._.._..Глуб,
Глуб).
восст_глуб(
ЧХ..Б..Л..Ч..Г, ЧХ..Б..Л..Ч..0).
% Формируется копия позиции, глубина
устанавливается в 0
% Некоторые отношения между клетками доски
сосед_чсл( N, N1) :-
%
Соседнее число "в пределах доски"
( N1 is N + 1;
N1 is N - 1 ),
внутри( N1).
внутри( N) :-
N > 0, N < 9.
сосед_диаг( X : Y, X1 : Y1)
:-
% Соседние клетки по диагонали
сосед_чсл( X, X1 ), сосед_чсл( Y, Y1).
сосед_верт( X : Y, X : Y1)
:-
% Соседние клетки по вертикали
сосед_чсл( Y, Y1).
сосед_гор( X : Y, X1 : Y) :-
% Соседние клетки по горизонтали
сосед_чсл( X, X1).
сосед( S, S1) :-
% Соседние клетки (предпочтение - диагонали)
сосед_диаг( S, S1);
сосед_гор( S, S1);
сосед_верт( S, S1).
конец_игры( Поз) :-
мат( Поз).
% Предикаты, ограничивающие ходы
% Специализированное генераторы ходов вида:
% ход( Ограничение, Поз, Ход, Поз1)
ход( глубина <
Макс, Поз, Ход, Поз1) :-
глуб( Поз, Г),
Г < Макс, !.
ход( глубина = Г, Поз,
Ход, Поз1) :-
глуб( Поз, Г), !.
ход( сначала диаг,
б..Б..Л..Ч..Г, Б-Б1,
ч..Б1..Л..Ч..Г1) :-
Г1 is Г + l,
сосед( Б, Б1),
%
"сосед" порождает сначала диагональные ходы
not сосед( Б1, Ч),
% Не попасть под шах
Б1 \== Л.
% Не столкнуться с ладьей
ход( ход ладьей,
б..Б..Лх : Лу..Ч..Г, Лх : Лу-Л,
ч..Б..Л..Ч..Г1) :-
Г1 is Г + 1,
коорд( I),
% Число между 1 и 8
( Л = Лх : I; Л = I : Лу),
% По горизонтали или по вертикали
Л \== Лх : Лу,
%
Обязательно двигаться
not мешает( Лх : Лу, Б, Л).
% Мешает белый король
ход( ход_шах, Поз,
Л-Лх : Лу, Поз1) :-
бл( Поз, Л),
чк( Поз, Чх : Чу),
( Лх = Чх; Лу = Чу),
% Ладья и черный король на одной линии
ход( ход_ладьей, Поз, Л-Лх : Лу, Поз1).
ход( разреш, б..П, М,
П1) :-
( Огр = сначала_диаг; Огр = ход ладьей),
ход( Огр, б..П, М, П1).
ход( разреш,
ч..Б..Л..Ч..Г, Ч-Ч1, б..Б..Л..Ч1..Г1) :-
Г1 is Г + 1,
сосед( Ч, Ч1),
not шах( б..Б..Л..Ч1..Г1).
разрход( Поз, Ход,
Поз1) :-
ход( разреш, Поз, Ход, Поз1).
шах( _..Б..Лх : Лу..Чх :
Чу.._ ) :-
сосед( Б, Чх : Чу);
% Короли
рядом
( Лх = Чх; Лу = Чу),
Лх : Лу \== Чх : Чу,
% Нет
взятия ладьи
not мешает( Лх : Лу, Б, Чх : Чу).
мешает( S, S1, S1) :- !.
мешает( X1 : Y, X2 : Y, Х3 :
Y) :-
упоряд( X1, Х2, Х3), !.
мешает( X : Y1, X : Y2, X :
Y3) :-
упоряд( Y1, Y2, Y3).
упоряд( N1, N2, N3) :-
N1 < N2, N2 < N3;
N3 < N2, N2 < N1.
коорд( 1). коорд( 2). коорд( 3). коорд( 4).
коорд( 5). коорд( 6). коорд( 7). коорд( 8).
% Предикаты целей
любая_поз( Поз).
ход_противника( б.._ ). % Противник ходит белыми
мат( Поз) :-
чей_ход( Поз, ч),
шах( Поз),
not разрход( Поз, _, _ ).
пат( Поз) :-
чей_ход( Поз, ч),
not шах( Поз),
not разрход( Поз, _, _ ).
уменьш_простр( Поз,
КорнПоз) :-
простр( Поз, Пр),
простр( КорнПоз, КорнПр),
Пр < КорнПр.
ладья_под_боем(
ЧейХод..Б..Л..Ч.._ ) :-
расст( Б, Л, Р1),
расст( Ч, Л, Р2),
( ЧейХод = б, !, Р1 > Р2 + 1;
ЧейХод = ч, !, Р1 > Р2 ).
ближе_к_клетке( Поз,
КорнПоз) :-
расст_до_клетки( Поз, Р1),
расст_до_клетки( КорнПоз, Р2),
Р1 < Р2.
расст_до_клетки(
Поз, Мрасст) :-
% Манхеттеновское
расстояние
бк( Поз, БК),
% между БК и
критической клеткой
кк( Поз, КК),
% Критическая клетка
манх_расст( БК, КК, Мрасст).
раздел( _..Бх : Бу..Лх :
Лу.. Чх : Чу.._ ) :-
упоряд( Бх, Лх, Чх), !;
упоряд( Бу, Лу, Чу).
l_конфиг( _..Б..Л..Ч.._ )
:-
%
L - конфигурация
манх_расст( Б, Ч, 2),
манх_расст( Л, Ч, 3).
не дальше_от_ладьи(
_..Б..Л.._, _..Б1..Л1.._ ) :-
расст( Б, Л, Р),
расст( Б1, Л1, Р1),
Р =< Р1.
простр_больше_2( Поз)
:-
простр( Поз, Пр),
Пр > 2.
наш_король_на_краю(
_..Х : Y.._ ) :-
% Белый король
на краю
( X = 1, !; X = 8, !; Y = 1, !; Y = 8).
король_противника_на_краю(
_..Б..Л..Х : Y.._ ) :-
% Черный король
на краю
( X = 1, !; X = 8, !; Y = 1, !; Y = 8).
короли_рядом( Поз) :-
% Расстояние между королями < 4
бк( Поз, БК), чк( Поз, ЧК),
расст( БК, ЧК, Р),
Р < 4.
потеря_ладьи( _..Б..Л..Л.._ )- % Ладья взята
потеря_ладьи(
ч..Б..Л..Ч.._ ) :-
сосед( Ч, Л),
% Черный король напал
на ладью
not сосед( Б, Л).
% Белый король не защищает ладью
расст( X : Y, X1 : Y1, Р) :-
%
Расстояние до короля
абс_разн( X, X1, Рх),
абс_разн( Y, Y1, Ру),
макс( Рх, Ру, Р).
абс_разн( А, В, С) :-
А > В, !, С is A - В;
С is В - А.
макс( А, В, М) :-
А >= В, !, М = А;
М = В.
манх_расст( X : Y, X1 : Y1, Р) :- % Манхеттеновское расстояние
абс_разн( X, X1, Рх),
абс_разн( Y, Y1, Ру),
P is Рх + Ру.
простр( Поз, Пр) :-
% Область, в которой "заперт" черный
король
бл( Поз, Лх : Лу),
чк( Поз, Чх : Чу),
( Чх < Лх, СторонаХ is Лх - 1;
Чх > Лх, СторонаХ is 8 - Лх ),
( Чу < Лу, СторонаY is Лу - 1;
Чу > Лу, СторонаY is 8 - Лу ),
Пр is СторонаХ * СторонаY, !;
Пр = 64. % Ладья и черный
король на одной линии
кк( _..Б..Лх : Лу.. Чх :
Чу.._, Кх : Ку) :-
% Критическая клетка
( Чх < Лх, !, Кх is Лх - 1; Кх is Лх + 1),
( Чу < Лу, !, Ку is Лу - 1; Ку is Лу + 1).
% Процедуры для отображения позиций
отобр( Поз) :-
nl,
коорд( Y), nl,
коорд( X),
печ_фиг( X : Y, Поз),
fail.
отобр( Поз) :-
чей_ход( Поз, ЧХ), глуб( Поз, Г),
nl, write( 'ЧейХод='), write( ЧХ),
write( 'Глубина='), write( Г), nl.
печ_фиг( Клетка,
Поз):-
бк( Поз, Клетка), !, write( 'Б');
бл( Поз, Клетка), !, write( 'Л');
чк( Поз, Клетка), !, write( 'Ч');
write( '.').
показать_ход( Ход) :-
nl, write( Ход), nl.
Рис. 15. 10. Библиотека предикатов для окончания "король и ладья против короля".
Минимаксный принцип, реализованный в форме альфа-бета алгоритма, - это наиболее популярный метод в игровом программировании. Особенно часто он применяется в шахматных программах. Минимаксный принцип был впервые предложен Шенноном (Shannon 1950). Возникновение и становление альфа-бета алгоритма имеет довольно запутанную историю. Несколько исследователей независимо друг от друга открыли либо реализовали этот метод полностью или частично. Эта интересная история описана в статье Knuth and Moore (1978). Там же приводится более компактная формулировка альфа-бета алгоритма, использующая вместо минимаксного принципа принцип "него-макса" ("neg-max" principle), и приводится математический анализ производительности алгоритма. Наиболее полный обзор различных минимаксных алгоритмов вместе с их теоретическим анализом содержится в книге Pearl (1984). Существует еще один интересный вопрос, относящийся к минимаксному принципу. Мы знаем, что статическим оценкам следует доверять только до некоторой степени. Можно ли считать, что рабочие оценки являются более надежными, чем исходные статические оценки, из которых они получены? В книге Pearl (1984) собран ряд математических результатов, имеющих отношение к ответу на этот вопрос. Приведенные в этой книге результаты, касающиеся распространения ошибок по минимаксному дереву, объясняют, в каких случаях и почему минимаксный принцип оказывается полезным.
Сборник статей Bramer (1983) охватывает несколько аспектов игрового программирования. Frey (1983) - хороший сборник статей по шахматным программам. Текущие разработки в области машинных шахмат регулярно освещаются в серии Advances in Computer Chess и в журнале ICCA.
Метод Языка Советов, позволяющий использовать знания о типовых ситуациях, был предложен Д. Мики. Дальнейшее развитие этого метода отражено в Bratko and Michi (1980 a, b) и Bratko (1982, 1984, 1985). Программа для игры в эндшпиле "король и ладья против короля", описанная в этой главе, совпадает с точностью до незначительных модификаций с таблицей советов, корректность которой была математически доказана в статье Bratko (1978). Ван Эмден также запрограммировал эту таблицу советов на Прологе (van Emden 1982).
Среди других интересных экспериментов в области машинных шахмат, преследующих цель повысить эффективность знаний (а не перебора), следует отметить Berliner (1977), Pitrat (1977) и Wilkins (1980).
Advances in Computer Chess Series (M.R.B. Clarke, ed). Edinburgh University Press (Vols. 1-2), Pergamon Press (Vol. 3).
Berliner M. A. (1977); A representation and some mechanisms for a problem solving chess program. In: Advances in Computer Chess 1 (M.R.B. Clarke, ed). Edinburgh University Press.
Bramer M. A; (1983, ed). Computer Game Playing: Theory and Practice. Ellis Horwood and John Wiley.
Bratko I. (1978) Proving correctness of strategies in the AL1 assertional language. Information Processing Letters 7: 223-230.
Bratko I. (1982). Knowledge-based problem solving in AL3. In: Machine Intelligence 10 (J. Hayes, D. Michie, J. H. Pao, eds.). Ellis Horwood (an abbreviated version also appears in Bramer 1983).
Bratko I. (1984). Advise and planning in chess end-games. In: Artificial and Human Intelligence (S. Amarel, A. Elithorn, R. Banerji, eds.). North-Holland.
Bratko I. (1985). Symbolic derivation of chess patterns. In: Progress Artificial Intelligence (L. Steels, J. A. Campbell, eds.). Ellis Horwood and John Wiley.
Bratko I. and Michie D. (1980a). A representation of pattern-knowledge in chess end-games. In: Advances in Computer Chess 2 (M.R.B. Clarke, ed). Edinburgh University Press.
Bratko I. and Michie D. (1980b). An advice program for a complex chess programming task. Computer Journal 23: 353-359.
Frey P. W. (1983, ed.). Chess Skill in Man and Machine (second edition). Springer-Verlag.
Knuth D. E. and Moore R. W. (1975). An analysis of alpha-beta pruning. Artificial Intelligence 6: 93-326.
Pearl J. (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley.
Pitrat J. (1977). A chess combination program which uses plans Artificial Intelligence 8: 275-321.
Shannon C.E. (1950). Programming a computer for playing chess. Philosophical Magazine 41: 256-275. [В сб. Шеннон К. Работы по теории информации и кибернетике. - М.: ИЛ., 1963.]
van Emden M. (1982). Chess end-game advice: a case study in computer utilisation of knowledge. In: Machine Intelligence 10 (J. Hayes, D. Michie, J.H. Pao, eds). Ellis Hordwood.
Wilkins D.E. (1980). Using patterns and plans in chess. Artificial Intelligence 14: 165-203.
Назад | Содержание | Вперёд