Назад | Содержание | Вперёд
В настоящем разделе мы реализуем простую программу для
автоматического доказательства теорем в виде системы, управляемой образцами. Эта программа будет основана на принципе резолюции - популярном методе, обычно используемом в машинном доказательстве теорем. Мы ограничимся случаем пропозициональной логики, поскольку нашей целью будет дать всего лишь простую иллюстрацию используемого принципа. На самом деле, принцип резолюции можно легко обобщить на случай исчисления высказываний первого порядка (с применением логических формул, содержащих переменные). Базовый Пролог можно рассматривать как частный случай системы доказательства теорем, основанной на принципе резолюции.Задачу доказательства теорем можно сформулировать так: дана формула, необходимо показать, что эта формула является теоремой, т. е. она верна всегда, независимо от интерпретации встречающихся в ней символов. Например, утверждение, записанное в виде формулы
р v ~ р
и означающее "р или не р", верно всегда, независимо от смысла утверждения р.
Мы будем использовать в качестве операторов следующие символы:
~
отрицание, читается как "не"
&
конъюнкцию, читается как "и"
v
дизъюнкцию, читается как "или"
=> импликацию,
читается как "следует"
Согласно правилам предпочтения операторов, оператор "не" связывает утверждения сильнее, чем "и", "или" и "следует".
Метод резолюции предполагает, что мы рассматриваем отрицание исходной формулы и пытаемся показать, что полученная формула противоречива. Если это действительно так, то исходная формула представляет собой тавтологию. Таким образом, основную идею можно сформулировать так: доказательство противоречивости формулы с отрицанием эквивалентно доказательству того, что исходная формула (без отрицания) есть теорема (т. е. верна всегда). Процесс, приводящий к искомому противоречию, состоит из отдельных шагов, на каждом из которых применяется резолюция.
Давайте проиллюстрируем этот принцип на примере. Предположим, что мы хотим доказать, что теоремой является следующая пропозициональная формула:
(а => b) & (b => с) => (а => с)
Смысл этой формулы таков: если из а следует b и из b следует с, то из а следует с.
Прежде чем начать применять процесс резолюции ("резолюционный процесс"), необходимо представить
отрицание нашей формулы в наиболее приспособленной для этого форме. Такой формой является конъюнктивная нормальная форма, имеющая вид (р1 v p2
v ...) & (q1 v q2
v ...)
& (r1 v r2 v
...) & ...
Здесь рi, qi, ri - элементарные утверждения
или их отрицания. Конъюнктивная нормальная форма есть конъюнкция членов, называемых дизъюнктами, например (p1 v p2 v ...) - это дизъюнкт.Любую пропозициональную формулу нетрудно преобразовать в такую форму. В нашем случае это делается следующим образом. У нас есть исходная формула
(а => b) & (b => с) => (а => с)
Ее отрицание имеет вид
~ ( (а => b) & (b => с) => (а => с) )
Для преобразования этой формулы в конъюнктивную нормальную форму можно использовать следующие известные правила:
(1) х =>
у
эквивалентно
~х v у
(2) ~(x
v y)
эквивалентно
~х & ~у
(3) ~(х
& у)
эквивалентно
~х v ~у
(4) ~( ~х)
эквивалентно
х
Применяя правило 1, получаем
~ ( ~ ( (a => b) & (b => с)) v (а => с) )
Далее, правила 2 и 4 дают
(а => b) & (b => с) & ~(а => с)
Трижды применив правило 1, получаем
(~ а v b) & (~b v с) & ~(~а v с)
И наконец, после применения правила 2 получаем искомую конъюнктивную нормальную форму
(~а v b) & (~b v с) & а & ~с
состоящую из четырех дизъюнктов. Теперь можно приступить к резолюционному процессу
.Элементарный шаг резолюции выполняется всегда, когда имеется два дизъюнкта, в одном из которых встретилось элементарное утверждение р, а в другом - ~р. Пусть этими двумя дизъюнктами будут
р v Y и ~р v
ZШаг резолюции порождает третий дизъюнкт:
Y v Z
Нетрудно показать, что этот дизъюнкт логически следует из тех двух дизъюнктов, из которых он получен. Таким образом, добавив выражение (Y v Z) к нашей исходной формуле, мы не изменим ее истинности. Резолюционный процесс порождает новые дизъюнкты. Появление "пустого дизъюнкта" (обычно записываемого как "nil") сигнализирует о противоречии. Действительно, пустой дизъюнкт nil порождается двумя дизъюнктами вида
x и ~x
которые явно противоречат друг другу.

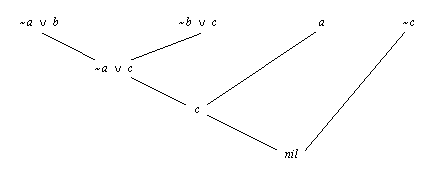
Рис. 16. 6.
Доказательство теоремы (а=>b)&(b=>с)=>(a=>с)
методом
резолюции. Верхняя строка - отрицание теоремы в
конъюнктивной
нормальной форме. Пустой дизъюнкт внизу
сигнализирует, что
отрицание теоремы противоречиво.
На рис. 16.6 показан процесс применения резолюций, начинающийся с отрицания нашей предполагаемой теоремы и заканчивающийся пустым дизъюнктом.
На рис. 16.7 мы видим, как резолюционный процесс можно сформулировать в форме программы, управляемой образцами. Программа работает с дизъюнктами, записанными в базе данных. В терминах образцов принцип резолюции формулируется следующим образом:
если
существуют два таких дизъюнкта С1
и С2, что
P является (дизъюнктивным)
подвыражением С1,
а ~Р - подвыражением С2
то
удалить Р из С1 (результат
- СА), удалить ~Р
из С2 (результат - СВ) и
добавить в базу
данных новый дизъюнкт СА v СВ.
На нашем формальном языке это можно записать так:
[ дизъюнкт( С1),
удалить( Р, Cl, CA),
дизъюнкт( С2),
удалить( ~Р, С2, СВ) ] --->
[ assert( дизъюнкт( СА v СВ) ) ].
Это правило нуждается в небольшой доработке. Дело в том, что мы не должны допускать повторных взаимодействий между дизъюнктами, так как они порождают новые копии уже существующих формул. Для этого в программе рис. 16.7 предусматривается запись в базу данных информации об уже произведенных взаимодействиях в форме утверждений вида
сделано( Cl, C2, Р)
В условных частях правил производится распознавание подобных утверждений и обход соответствующих повторных действий.
Правила, показанные на рис. 16.7, предусматривают также обработку специальных случаев, в которых требуется избежать явного представления пустого дизъюнкта. Кроме того, имеются два правила для упрощения дизъюнктов. Одно из них убирает избыточные подвыражения. Например, это правило превращает выражение
a v b v a
в более простое выражение a v b. Другое правило распознает те дизъюнкты, которые всегда истинны, например,
a v b v ~а
и удаляет их из базы данных, поскольку они бесполезны при поиске противоречия.
% Продукционные правила для задачи
автоматического
% доказательства теорем
% Противоречие
[ дизъюнкт( X),
дизъзюнкт( ~Х) ] --->
[ write( 'Обнаружено
противоречие'), стоп].
% Удалить тривиально истинный дизъюнкт
[ дизъюнкт( С),
внутри( Р, С), внутри( ~Р, С) ] --->
[ retract( С) ].
% Упростить дизъюнкт
[ дизъюнкт( С),
удалить( Р, С, С1), внутри( Р, С1) ] --->
[ заменить( дизъюнкт( С),
дизъюнкт( С1) ) ].
% Шаг резолюции, специальный случай
[ дизъюнкт( Р),
дизъюнкт( С), удалить( ~Р, С, С1),
not сделано( Р, С, Р) ] --->
[ аssеrt( дизъюнкт( С1)), аssert(
сделано( Р, С, Р))].
% Шаг резолюции, специальный случай
[ дизъюнкт( ~Р),
дизъюнкт( С), удалить( Р, С, С1),
not сделано( ~Р, С, Р) ] --->
[ assert( дизъюнкт( C1)), аssert(
сделано( ~Р, С, Р))].
% Шаг резолюции, общий случай
[ дизъюнкт( С1),
удалить( Р, С1, СА),
дизъюнкт( С2),
удалить( ~Р, С2, СВ),
not сделано( Cl, C2, Р) ]
--->
[ assert( дизъюнкт( СА v СВ) ),
assert( сделано( Cl, C2, Р)
) ].
% Последнее правило: тупик
[ ] ---> [ write( 'Нет противоречия'), стоп ].
% удалить( Р, Е, Е1) означает, получить из
выражения Е
% выражение Е1, удалив из него подвыражение Р
удалить( X, X v Y, Y).
удалить( X, Y v X, Y).
удалить( X, Y v Z, Y v Z1) :-
удалить( X, Z, Z1).
удалить( X, Y v Z, Y1 v Z) :-
удалить( X, Y, Y1).
% внутри( Р, Е) означает Р есть дизъюнктивное
подвыражение
% выражения Е
внутри( X, X).
внутри( X, Y) :-
удалить( X, Y, _ ).
Рис. 16. 7. Программа,
управляемая образцами, для
автоматического доказательства теорем.
Остается еще один вопрос: как преобразовать заданную пропозициональную формулу в конъюнктивную нормальную форму? Это несложное преобразование выполняется с помощью программы, показанной на рис. 16.8. Процедура
транс( Формула)
транслирует заданную формулу в множество дизъюнктов Cl, C2 и т.д. и записывает их при помощи assert в базу данных в виде утверждений
дизъюнкт( С1).
дизъюнкт( С2).
. . .
Программа, управляемая образцами, для автоматического доказательства теорем запускается при помощи цели пуск. Таким образом, для того чтобы доказать при помощи этой программы некоторую теорему, мы транслируем ее отрицание в конъюнктивную нормальную форму, а затем запускаем резолюционный процесс. В нашем примере это можно сделать так:
% Преобразование пропозициональной формулы
в множество
% дизъюнктов с записью их в базу данных при помощи
assert
:- ор( 100, fy, ~).
% Отрицание
:- ор( 110, xfy, &).
% Конъюнкция
:- ор( 120, xfy, v).
% Дизъюнкция
:- ор( 130, xfy, =>).
% Импликация
транс( F & G) :- !,
% Транслировать конъюнктивную формулу
транс( F),
транс( G).
транс( Формула) :-
тр( Формула, НовФ), !,
% Шаг трансформации
транс( НовФ).
транс( Формула) :-
%
Дальнейшая трансформация невозможна
assert( дизъюнкт( Формула) ).
% Правила трансформаций для пропозициональных формул
тр( ~( ~Х), X) :- !. % Двойное отрицание
тр( X => Y, ~Х v Y) :- !. % Устранение импликации
тр( ~( X & Y), ~Х v ~Y) :- !. % Закон де Моргана
тр( ~( X v Y), ~Х & ~Y) :- !. % Закон де Моргана
тр( X & Y v Z, (X v Z) &
(Y v Z) ) :- !.
% Распределительный закон
тр( X v Y & Z, (X v Y) &
(X v Z) ) :- !.
% Распределительный закон
тр( X v Y, X1 v Y) :-
%
Трансформация подвыражения
тр( X, X1), !.
тр( X v Y, X v Y1) :-
%
Трансформация подвыражения
тр( Y, Y1), !.
тр( ~Х, ~Х1) :-
% Трансформация подвыражения
тр( X, X1).
Рис. 16. 8.
Преобразование пропозициональных формул в
множество
дизъюнктов с записью их в базу данных при помощи assert.
?- транс( ~(( а=>b) & ( b=>c) => ( а=>с)) ), пуск.
Ответ программы "Обнаружено противоречие" будет означать, что исходная формула является теоремой.
Назад | Содержание | Вперёд