Назад | Содержание | Вперёд
Эта задача состоит в отыскании такой расстановки восьми ферзей на пустой шахматной доске, в которой ни один из ферзей не находится под боем другого. Решение мы запрограммируем в виде унарного отношения:
решение( Поз)
которое истинно тогда и только тогда, когда Поз изображает позицию, в которой восемь ферзей не бьют друг друга. Будет интересно сравнить различные идеи, лежащие в основе программирования этой задачи. Поэтому мы приведем три программы, основанные на слегка различающихся ее представлениях.
4. 5. 1. Программа 1
Вначале нужно выбрать способ представления позиции на доске. Один из наиболее естественных способов - представить позицию в виде списка из восьми элементов, каждый из которых соответствует одному из ферзей. Каждый такой элемент будет описывать то поле доски, на которой стоит соответствующий ферзь. Далее, каждое поле доски можно описать с помощью пары координат ( Х и Y), где каждая координата - целое число от 1 до 8. В программе мы будем записывать такую пару в виде
Х / Y
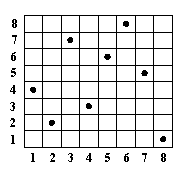
где оператор "/" обозначает, конечно, не деление, а служит лишь для объединения координат поля в один элемент списка. На рис. 4.6 показано одно из решений задачи о восьми ферзях и его запись в виде списка.
После того. как мы выбрали такое представление, задача свелась к нахождению списка вида:
[Xl/Yl, X2/Y2, X3/Y3, X4/Y4, X5/Y5, X6/Y6, X7/Y7, X8/Y8]
удовлетворяющего требованию отсутствия нападений. Наша процедура решение должна будет найти подходящую конкретизацию переменных X1, Y1, Х2, Y2, ..., Х8, Y8. Поскольку мы знаем, что все ферзи должны находиться на разных вертикалях во избежание нападений по вертикальным линиям, мы можем сразу же ограничить перебор, чтобы облегчать поиск решения. Можно поэтому сразу зафиксировать Х-координаты так, чтобы список, изображающий решение, удовлетворял следующему, более конкретному шаблону:
[1/Y1, 2/Y2, 3/Y3, 4/Y4, 5/Y5, 6/Y6, 7/Y7, 8/Y8]

Рис. 4. 6. Решение задачи
о восьми ферзях. Эта позиция может быть
представлена в виде списка [1/4, 2/2,
3/7, 4/3, 5/6, 6/8, 7/5, 8/1].
Нас интересует решение для доске размером 8х8. Однако, как это часто бывает в программировании, ключ к решению легче найти, рассмотрев более общую постановку задачи. Как это ни парадоксально, но часто оказывается, что решение более общей задачи легче сформулировать, чем решение более частной, исходной задачи; после этого исходная задача решается просто как частный случай общей задачи.
Основная часть работы при таком подходе ложится на нахождение правильного обобщения исходной задачи. В нашем случае хорошей является идея обобщать задачу в отношении количества ферзей (количества вертикалей в списке), разрешив количеству ферзей принимать любое значение, включая нуль. Тогда отношение решение можно сформулировать, рассмотрев два случая:
Случай 1. Список ферзей пуст. Пустой список без сомнения является решением, поскольку нападений в этом случае нет.
Случай 2. Список ферзей не пуст. Тогда он выглядит так:
[ X/Y | Остальные ]
В случае 2 первый ферзь находится на поле Х / Y, а остальные - на полях, указанных в списке Остальные. Если мы хотим, чтобы это было решением, то должны выполняться следующие условия:
(1) Ферзи, перечисленные в списке Остальные, не должны бить друг друга; т. е. список Остальные сам должен быть решением.
(2) Х и Y должны быть целыми числами от 1 до 8.
(3) Ферзь, стоящий на поле X / Y, не должен бить ни одного ферзя из списка Остальные.
Чтобы запрограммировать первое условие, можно воспользоваться самим отношением решение. Второе условие можно сформулировать так: Y должен принадлежать списку целых чисел от 1 до 8. т. е. [1, 2, 3, 4, 5, 6, 7, 8]. С другой стороны, о координате Х можно не беспокоиться, поскольку список-решение должен соответствовать шаблону, у которого Х-координаты уже определены. Поэтому Х гарантированно получит правильное значение от 1 до 8. Третье условие можно обеспечить с помощью нового отношения небьет. Все это можно записать на Прологе так:
решение( [X/Y |
Остальные] ) :-
решение( Остальные),
принадлежит( Y, [1, 2, 3, 4, 5, 6, 7, 8] ),
небьет( X/Y, Остальные).
Осталось определить отношение небьет:
небьет( Ф, Фспис)
И снова его описание можно разбить на два случая:
(1) Если список Фспис пуст, то отношение, конечно, выполнено, потому что некого бить (нет ферзя, на которого можно было бы напасть).
(2) Если Фспис не пуст, то он имеет форму
[Ф1 | Фспис1]
и должны выполняться два условия:
(а) ферзь на поле Ф не должен бить ферзя на поле Ф1 и
(b) ферзь на поле Ф не должен бить ни одного ферзя из списка Фспис1.
Выразить требование, чтобы ферзь, находящийся на некотором поле, не бил другое поле, довольно просто: эти поля не должны находиться на одной и той же горизонтали, вертикали или диагонали: Наш шаблон решения гарантирует, что все ферзи находятся на разных вертикалях, поэтому остается только обеспечить, чтобы
На рис. 4.7 приведен полный текст программы. Чтобы облегчить ее использование, необходимо добавить список-шаблон. Это можно сделать в запросе на генерацию решений. Итак:
?- шаблон( S), решение( S).
решение( [ ] ).
решение( [X/Y | Остальные ] ) :-
% Первый ферзь на поле X/Y,
% остальные ферзи на полях из списка Остальные
решение( Остальные),
принадлежит Y, [1, 2, 3, 4, 5, 6, 7,
8] ),
небьет( X/Y | Остальные).
% Первый ферзь не бьет остальных
небьет( _, [ ]). % Некого бить
небьет( X/Y, [X1/Y1 | Остальные] ) :-
Y =\= Y1,
% Разные Y-координаты
Y1-Y =\= X1-X
% Разные диагонали
Y1-Y =\= X-X1,
небьет( X/Y,
Остальные).
принадлежит( X, [X | L] ).
принадлежит( X, [Y | L] ) :-
принадлежит(
X, L).
% Шаблон решения
шаблон( [1/Y1, 2/Y2, 3/Y3, 4/Y4, 5/Y5, 6/Y6, 7/Y7, 8/Y8]).
Рис. 4. 7. Программа1 для задачи о восьми ферзях.
Система будет генерировать решения в таком виде:
S = [1/4, 2/2, 3/7, 4/3, 5/6, 6/8,
7/5, 8/1];
S = [1/5, 2/2, 3/4, 4/7, 5/3, 6/8, 7/6, 8/1];
S = [1/3, 2/5, 3/2, 4/8, 5/6, 6/4, 7/7, 8/1].
. . .
4. 6. При поиске решения программа, приведенная на рис. 4.7, проверяет различные значения Y-координат ферзей. В каком месте программы задается порядок перебора альтернативных вариантов? Как можно без труда модифицировать программу, чтобы этот порядок изменился? Поэкспериментируйте с разными порядками, имея в виду выяснить, как порядок перебора альтернатив влияет на эффективность программы.
В соответствии с принятым в программе 1 представлением доски каждое решение имело вид
[1/Y1, 2/Y2, 3/Y3, ..., 8/Y8]
так как ферзи расставлялись попросту в последовательных вертикалях. Никакая информация не была бы потеряна, если бы Х-координаты были пропущены. Поэтому можно применить более экономное представление позиции на доске, оставив в нем только Y-координаты ферзей:
[Y1, Y2, Y3, ..., Y8]
Чтобы не было нападений по горизонтали, никакие два ферзя не должны занимать одну и ту же горизонталь. Это требование накладывает ограничение на Y-координаты: ферзи должны занимать все горизонтали с 1-й по 8-ю. Остается только выбрать порядок следования этих восьми номеров. Каждое решение представляет собой поэтому одну из перестановок списка:
[1, 2, 3, 4, 5, 6, 7, 8]
Такая перестановка S является решением, если каждый ферзь в ней не находится под боем (список S - "безопасный"). Поэтому мы можем написать:
решение( S) :-
перестановка( [1, 2, 3, 4, 5, 6, 7, 8], S),
безопасный( S).
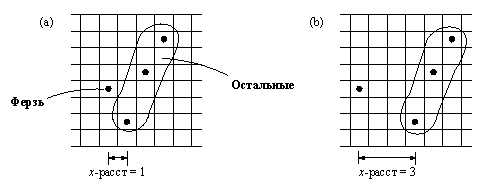
Рис. 4. 8. (а)
Расстояние по Х между Ферзь и Остальные
равно 1.
(b) Расстояние по Х между Ферзь
и Остальные равно 3
Отношение перестановка мы уже определила в гл. 3, а вот отношение безопасный нужно еще определить. Это определение можно разбить на два случая:
(1) S - пустой список. Тогда он, конечно, безопасный, ведь нападать не на кого.
(2) S - непустой список вида [Ферзь | Остальные]. Он безопасный, если список Остальные - безопасный и Ферзь не бьет ни одного ферзя из списка Остальные.
На Прологе это выглядит так:
безопасный( [ ]).
безопасный( [Ферзь |
Остальные ] :-
безопасный( Остальные),
небьет(Ферзь | Остальные).
В этой программе отношение небьет более хитрое.
решение( Ферзи) :-
перестановка( [1, 2, 3, 4, 5, 6, 7,
8], Ферзи),
безопасный( Ферзи).
перестановка( [ ], [ ]).
перестановка( [Голова | Хвост], СписПер) :-
перестановка( Хвост,
ХвостПер),
удалить( Голова, СписПер,
ХвостПер).
% Вставка головы в переставленный хвост
удалить( А, [А | Список).
удалять( А, [В | Список], [В, Список1] ) :-
удалить( А, Список,
Список1).
безопасный( [ ]).
безопасный( [Ферзь | Остальные]) :-
безопасный( Остальные),
небьет( Ферзь, Остальные,
1).
небьет( _, [ ], _ ).
небьет( Y, [Y1 | СписY], РасстХ) :-
Y1-Y =\= РасстХ,
Y-Y1 =\= РасстХ,
Расст1 is РасстХ + 1,
небьет( Y, СписY, Расст1).
Рис. 4. 9. Программа 2 для задачи о восьми ферзях.
Трудность состоит в том, что расположение ферзей определяется только их Y-координатами, а Х-координаты в представлении позиции не присутствуют в явном виде. Этой трудности можно избежать путем небольшого обобщения отношения небьет, как это показано на рис. 4.8. Предполагается, что цель
небьет( Ферзь, Остальные)
обеспечивает отсутствие нападении ферзя Ферзь на поля списка Остальные в случае, когда расстояние по Х между Ферзь и Остальные равно 1. Остается рассмотреть более общий случай произвольного расстояния. Для этого мы добавим его в отношение небьет в качестве третьего аргумента:
небьет( Ферзь, Остальные, РасстХ)
Соответственно и цель небьет в отношении безопасный должна быть изменена на
небьет( Ферзь, Остальные, 1)
Теперь отношение небьет может быть сформулировано в соответствии с двумя случаями, в зависимости от списка Остальные: если он пуст, то бить некого и, естественно, нет нападений; если же он не пуст, то Ферзь не должен бить первого ферзя из списка Остальные (который находится от ферзя Ферзь на расстоянии РасстХ вертикалей), а также ферзей из хвоста списка Остальные, находящихся от него на расстоянии РасстХ + 1. Эти соображения приводят к программе, изображенной на рис. 4.9.
Наша третья программа для задачи о восьми ферзях опирается на следующие соображения. Каждый ферзь должен быть размещен на некотором поле, т. е. на некоторой вертикали, некоторой горизонтали, а также на пересечении каких-нибудь двух диагоналей. Для того, чтобы была обеспечена безопасность каждого ферзя, все они должны располагаться в разных вертикалях, разных горизонталях и в разных диагоналях (как идущих сверху вниз, так и идущих снизу вверх). Естественно поэтому рассмотреть более богатую систему представления с четырьмя координатами:
x
вертикали
у
горизонтали
u
диагонали, идущие снизу вверх
v
диагонали, идущие сверху вниз
Эти координаты не являются независимыми: при заданных х и у, u и v определяются однозначно (пример на рис.4.10). Например,
u = х - у
v = х + у
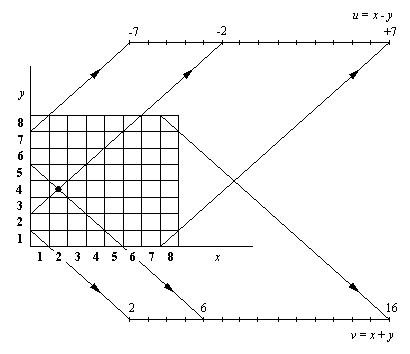
Рис. 4. 10. Связь между
вертикалями, горизонталями и диагоналями. Помеченное
поле имеет следующие координаты: x
= 2, у = 4, u = 2 - 4 = -2, v = 2 + 4 = 6.
Области изменения всех четырех координат таковы:
Dx = [1, 2, 3, 4, 5, 6, 7, 8]
Dy = [1, 2, 3, 4, 5, 6, 7, 8]
Du = [-7, -6, -5, -4, -3, -2, -1, 0,
1, 2, 3, 4, 5, 6, 7]
Dv = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16]
Задачу о восьми ферзях теперь можно сформулировать следующим образом: выбрать восемь четверок (X, Y, U, V), входящих в области изменения (X в Dx, Y в Dy и т.д.), так, чтобы ни один их элемент не выбирался дважды из одной области. Разумеется, выбор Х и Y определяет выбор U и V. Решение при такой постановке задачи может быть вкратце таким: при заданных 4-х областях изменения выбрать позицию для первого ферзя, вычеркнуть соответствующие элементы из 4-х областей изменения, а затем использовать оставшиеся элементы этих областей для размещения остальных ферзей. Программа, основанная на таком подходе, показана на рис. 4.11. Позиция на доске снова представляется списком Y-координат. Ключевым отношением в этой программе является отношение
peш( СписY, Dx, Dy, Du, Dv)
которое конкретизирует Y-координаты (в СписY) ферзей, считая, что они размещены в последовательных вертикалях, взятых из Dx. Все Y-координаты и соответствующие координаты U и V берутся из списков Dy, Du и Dv. Главную процедуру решение можно запустить вопросом
?- решение( S)
Это вызовет запуск реш с полными областями изменения координат, что соответствует пространству
решение( СписY) :-
реш( СписY,
% Y-координаты ферзей
[1, 2, 3, 4, 5, 6, 7, 8],
% Область изменения Y-координат
[1, 2, 3, 4, 5, 6, 7, 8],
% Область изменения Х-координат
[-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7],
% Диагонали, идущие снизу вверх
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 14, 15, 16] ).
% Диагонали, идущие сверху вниз
реш([ ], [ ], Dy, Du, Dv).
реш( [Y | СписY], [X | Dx1], Dy, Du, Dv) :-
удалить( Y, Dy, Dy1),
% Выбор
Y-координаты
U is X-Y
% Соответствующая диагональ вверх
удалить( U, Du, Du1),
% Ее
удаление
V is X+Y
% Соответствующая диагональ вниз
удалить( V, Dv, Dv1),
% Ее
удаление
реш( СписY, Dх1, Dy1, Du1,
Dv1).
% Выбор из оставшихся значений
удалить( А, [А | Список], Список).
удалить(A, [В | Список ], [В | Список1 ] ) :-
удалить( А, Список,
Список1).
Рис. 4. 11. Программа 3 для задачи о восьми ферзях.
задачи о восьми ферзях.
Процедура реш универсальна в том смысле, что ее можно использовать для решения задачи об N ферзях (на доске размером N х N). Нужно только правильно задеть области Dx, Dy и т.д.
Удобно автоматизировать получение этих областей. Для этого нам потребуется процедура
генератор( Nl, N2, Список)
которая для двух заданных целых чисел Nl и N2 порождает список
Список = [Nl, Nl + 1, Nl + 2, ..., N2 - 1, N2]
Вот она:
генератор( N, N, [N]).
генератор( Nl, N2, [Nl |
Список]) :-
Nl < N2,
М is Nl + 1,
генератор( М, N2, Список).
Главную процедуру решение нужно соответствующим образом обобщить:
решение( N, S)
где N - это размер доски, а S - решение, представляемое в виде списка Y-координат N ферзей. Вот обобщенное отношение решение:
решение( N, S) :-
генератор( 1, N, Dxy),
Nu1 is 1 - N, Nu2 is N - 1,
генератор( Nu1, Nu2, Du),
Nv2 is N + N,
генератор( 2, Nv2, Dv),
реш( S, Dxy, Dxy, Du, Dv).
Например, решение задачи о 12 ферзях будет получено с помощью:
?- решение( 12, S).
S = [1, 3, 5, 8, 10, 12, 6, 11, 2, 7, 9, 4]
Три решения задачи о восьми ферзях показывают, как к одной и той же задаче можно применять различные подходы. Мы варьировали также и представление данных. В одних случаях это представление было более экономным, в других - более наглядным и, до некоторой степени, избыточным. К недостаткам более экономного представления можно отнести то, что какая-то информация всякий раз, когда она требовалась, должна была перевычисляться.
В некоторых случаях основным шагом к решению было обобщение задачи. Как ни парадоксально, но при рассмотрении более общей задачи решение оказывалось проще сформулировать. Принцип такого обобщения - стандартный прием программирования, и его можно часто применять.
Из всех трех программ третья лучше всего показывает, как подходить к общей задаче построения структуры из заданного множества элементов при наличии ограничений.
Возникает естественный вопрос: " Какая из трех программ наиболее эффективна?" В этом отношение программа 2 значительно хуже двух других, а эти последние - одинаковы. Причина в том, что основанная на перестановках программа 2 строит все перестановки, тогда как две другие программы способны отбросить плохую перестановку не дожидаясь, пока она будет полностью построена. Программа 3 наиболее эффективна. Она избегает некоторых арифметических вычислений, результаты которых уже сразу заложены в избыточное представление доски, используемое этой программой.
4. 7. Пусть поля доски представлены парами своих координат в виде X/Y, где как X, так и Y принимают значения от 1 до 8.
(а) Определите отношение ходконя( Поле1, Поле2), соответствующее ходу коня на шахматной доске. Считайте, что Поле1 имеет всегда конкретизированные координаты, в то время, как координаты поля Поле2 могут и не быть конкретизированы. Например:
?- ходконя( 1/1, S).
S = 3/2;
S = 2/3;
no (нет)
(b) Определите отношение путьконя( Путь), где Путь - список полей, представляющих соответствующую правилам игры последовательность ходов коня по пустой доске.
(с) Используя отношение путьконя, напишите вопрос для нахождения любого пути, состоящего из 4-х ходов, и начинающегося с поля 2/1, а заканчивающегося на противоположном крае доски (Y= 8). Этот путь должен еще проходить после второго хода через поле 5/4.
Примеры, рассмотренные в данном разделе, иллюстрируют некоторые достоинства и характерные черты программирования на Прологе:
Назад | Содержание | Вперёд