Назад | Содержание | Вперёд
Наша оболочка экспертной системы, описанная в
предыдущем разделе, может работать только с
такими вопросами (утверждениями), которые либо
истинны, либо ложны. Предметные области, в
которых на любой вопрос можно ответить
"правда" или "ложь", называются категорическими.
Наши правила базы знания (также, как и данные)
были категорическими, это были
"категорические импликации". Однако многие
области экспертных знаний не являются
категорическими. Как правило, в заключениях
эксперта много догадок (впрочем, высказанных с
большой уверенностью), которые обычно верны, но
могут быть и исключения. Как данные,
относящиеся к конкретной задаче, так и
импликации, содержащиеся в правилах, могут
быть не вполне определенными.
Неопределенность можно промоделировать,
приписывая утверждениям некоторые
характеристики, отличные от "истина" и
"ложь". Характеристики могут иметь свое
внешнее выражение в форме дескрипторов, таких,
как, например, верно, весьма вероятно, вероятно,
маловероятно, невозможно. Другой
способ: степень уверенности может выражаться в
форме действительного числа, заключенного в
некотором интервале,
например между 0 и 1 или между -5 и +5. Такую числовую
характеристику называют по-разному - "коэффициент определенности", "степень доверия" или "субъективная
уверенность". Более естественным было бы
использовать вероятности (в математическом
смысле слова), но попытки применить их на
практике приводят к трудностям. Происходит это
по следующим причинам:
Поэтому, даже если выбранная мера
правдоподобия лежит в интервале 0 и 1, более
правильным будет называть ее из осторожности
"субъективной уверенностью", подчеркивая
этим, что имеется в виду оценка, данная экспертом.
Оценки эксперта не удовлетворяют всем
требованиям теории вероятностей. Кроме того,
вычисления над такими оценками могут отличаться
от исчисления вероятностей. Но, несмотря на это,
они могут служить вполне адекватной моделью
того, как человек оценивает достоверность своих
выводов. Для работы в условиях неопределенности было
придумано множество различных механизмов. Мы
будем рассматривать здесь механизм,
используемый в системах Prospector и AL/X для
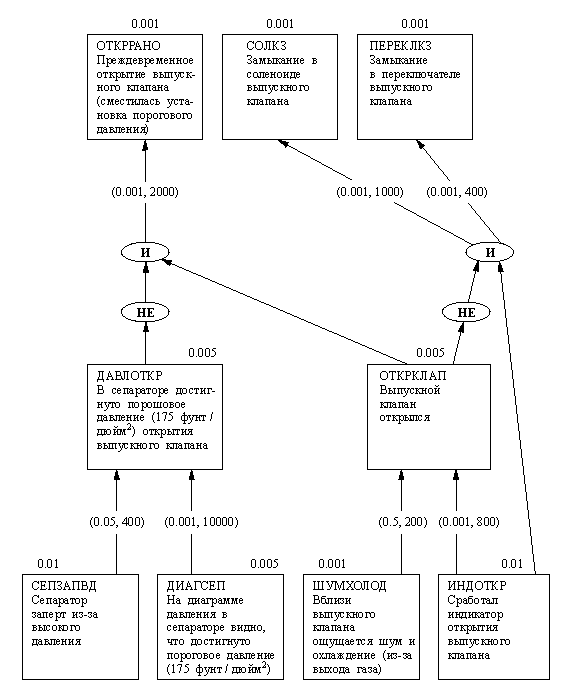
Достоверность событий моделируется с помощью действительных чисел, заключенных в интервале между 0 и 1. Для простоты изложения мы будем называть их "вероятностями", хотя более точный термин "субъективная уверенность". Отношения между событиями можно представить графически в форме "сети вывода". На рис. 14.14 показан пример сети вывода. События изображаются прямоугольниками, а отношения между ними - стрелками. Овалами изображены комбинации событий (И, ИЛИ, НЕ).
Мы будем считать, что отношения между событиями (стрелки) являются своего рода "мягкими импликациями". Пусть имеются два события E и H, и пусть информация о том, что имело место событие Е, оказывает влияние на нашу уверенность в том, что произошло событие H. Если это влияние является "категорической импликацией", то можно просто написать
если Е то H
В случае же "мягкой импликации" это отношение может быть менее определенным, так что ему можно приписать некоторую "силу", с которой оно действует:
если E то H с силой S
Та сила, с которой достоверность Е влияет на уверенность в H, моделируется в системе Prospector при помощи двух параметров:
N
= "коэффициент необходимости"
S =
"коэффициент достаточности"

Рис. 14. 14. Сеть вывода
системы AL/X (заимствовано
из Reiter (1980) ).
Числа, приписанные прямоугольникам, - априорные
вероятности событий; числами на стрелках
задается
"сила" отношений между событиями.
В сети вывода это изображается так:
E ------------> H
(N, S)
Два события, участвующие в отношении, часто называют "фактом" и "гипотезой" соответственно. Допустим, что мы проверяем гипотезу H. Тогда мы будем искать такой факт Е, который мог бы подтвердить либо опровергнуть эту гипотезу. S говорит нам, в какой степени достаточно факта Е для подтверждения гипотезы H; N - насколько необходим факт Е для подтверждения гипотезы Н. Если факт Е имел место, то чем больше S, тем больше уверенности в H. С другой стороны, если не верно, что имел место факт Е, то чем больше N, тем менее вероятно, что гипотеза H верна. В случае, когда степень достоверности Е находится где-то между полной достоверностью и невозможностью, степень достоверности H определяется при помощи интерполяции между двумя крайними случаями. Крайние случаи таковы:
(1) известно,
что факта Е не было
(2) известно, что
факт Е имел место
(3) ничего не
известно относительно Е
Для каждого события H сети вывода существует априорная вероятность р0(Н) (безусловная) вероятность события H в состоянии, когда неизвестно ни одного положительного или отрицательного факта. Если становится известным какой-нибудь факт E, то вероятность H меняет свое значение с р0(Н) на р(Н | Е). Величина изменения зависит от "силы" стрелки, ведущей из E в H. Итак, мы начинаем проверку гипотез, принимая их априорные вероятности. В дальнейшем происходит накопление информации о фактах, что находит свое отражение в изменении вероятностей событий сети. Эти изменения распространяются по сети от события к событию в соответствии со связями между событиями. Например, рассмотрим рис. 14.14 и предположим, что получена информация о срабатывании индикатора открытия выпускного клапана. Эта информация повлияет на нашу уверенность в том, что выпускной клапан открылся, что, в свою очередь, повлияет на уверенность в том, что сместилась установка порогового давления.
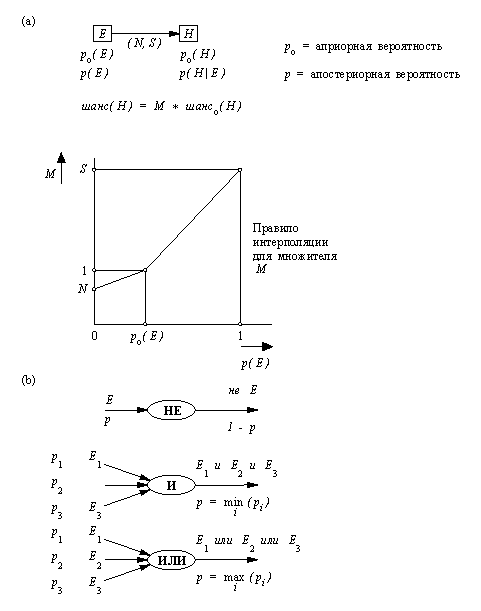
Рис. 14. 15. Правила
распространения вероятностей по сети,
принятые в системах Prospector и AL/X: (а)
"мягкая импликация"
с силой (N, S); (b) логические
комбинации отношений.
На рис. 14.15 показан один из способов реализации этого эффекта распространения информации по сети. Часть вычислений производится не над вероятностями, а над шансами. Это удобно, хотя в принципе и не обязательно. Между шансами и вероятностями имеет место простое соотношение:
шанс = вер / ( 1 -
вер)
вер = шанс / ( 1 + шанс)
Пусть между E и H существует отношение "мягкой импликации", тогда, в соответствии с рис. 14.15,
шанс (Н | Е) = М * шанс (H)
где множитель М определяется априорной и апостериорной вероятностями с учетом силы ( N, S) связи между E и H. Предполагается, что правила Prospector'a (рис. 14.15) для вычисления вероятностей логических комбинаций событий (использующие min и max) правильно моделируют поведение человека при оценке субъективной уверенности в таких составных событиях.
Давайте сначала расширим правила языка, с тем чтобы получить возможность работать с неопределенностью. К каждому, правилу мы можем добавить "силовой модификатор", определяемый двумя неотрицательными действительными числами S и N. Вот соответствующий формат:
Имя Правила:
если
Условие
то
Заключение
с
Сила( N, S).
Примеры правил рис. 14.14 можно изобразить в этой форме так:
прав1 :
если
не давлоткр и
открклап
то
открклрано
с
сила( 0.001, 2000).
прав2 :
если
сепзапвд
то
давлоткр
с
сила( 0.05, 400).
Для того, чтобы произвести соответствующее расширение оболочки экспертной системы (разд. 14.5), нам понадобится внести изменения в большинство процедур. Давайте сосредоточимся только на одной из них, а именно на процедуре
рассмотреть( Цель, Трасса, Ответ)
Мы предположим, что утверждение Цель не содержит переменных (как это сделано в Prospector'e и в AL/X). Это сильно упростит дело (особенно в процедуре ответпольз). Таким образом, Цель будет логической комбинацией элементарных утверждений. Например:
не давлоткр и открклап
Цепочку целей-предков и правил Трасса можно представить таким же способом, как это сделано в разд. 14.5. Однако форму представления объекта Ответ придется модифицировать для того, чтобы включить в нее вероятности. Цель и ее вероятность можно соединить в один терм следующим образом:
Цель : Вероятность
Получим такой пример объекта Ответ:
индоткр : 1 было сказано
Смысл ответа: пользователь сообщил системе, что событие индоткр произошло, и что это абсолютно достоверно.
Представление объекта Ответ требует еще одной модификации, в связи с тем, что в одно и то же событие могут вести несколько независимых связей, которые все окажут влияние на вероятность этого события - его шанс будет помножен (рис. 14.15) на все множители. В этом случае Ответ будет содержать список всех ветвей вывода заключения. Приведем пример ответа такого рода для сети рис. 14.14 (для наглядности расположенный на нескольких строках):
давлоткр : 1 было
'выведено по'
[ прав2 из сепзапвд : 1 было сказано,
прав5 из диагсеп : 1 было сказано ]
Процедура рассмотреть, выдающая ответы в такой форме, показана на рис. 14.16. Она обращается к предикату
импликация( Р0, Р, Сила, Вер0, Вер)
соответствующему отношению "мягкой импликации" (см. рис. 14.15). Р0 - априорная вероятность события Е, а Р - его апостериорная вероятность. Сила - сила импликации, представленная как
сила( N, S)
Вер0 и Вер - соответственно априорная и апостериорная вероятности гипотезы H.
Следует заметить, что наша реализация очень проста, она обеспечивает только изменение вероятностей при распространении информации по сети вывода и иногда ведет себя недостаточно разумно. Никакого внимания не уделяется отбору для анализа наиболее важной в данный момент информации. В более сложной версии следовало бы направлять процесс поиска ответа в сторону наиболее существенных фактов. Кроме того, необходимо стремиться к тому, чтобы пользователю задавалось как можно меньше вопросов.
Наконец, несколько замечаний относительно новой версии процедуры ответпольз. Она будет проще, чем процедура рис. 14.11, так как в запросах, передаваемых пользователю, уже не будет переменных. На этот раз пользователь в качестве ответа введет некоторую вероятность (вместо "да" или "нет"). Если пользователю ничего неизвестно о событии, содержащемся в вопросе, то вероятность этого события не изменится. Пользователь может также задать вопрос "почему" и получить изображение объекта Трасса в качестве объяснения. Кроме того, следует разрешить пользователю задавать вопрос: "Какова текущая вероятность моей гипотезы?" Тогда, если он устал вводить новую информацию (или у него мало времени), он может прекратить консультационный сеанс, довольствуясь ответом системы, полученным на основании неполной информации.
% Процедура
% рассмотреть( Цель, Трасса, Ответ)
%
% находит степень правдоподобия утверждения
"цель это правда".
% Оценка правдоподобия содержится в объекте
Ответ. Трасса - это
% цепочка целей-предшественников и правил,
которую можно
% использовать в объяснении типа "почему"
рассмотреть( Цель,
Трасса, ( Цель: Вер) было
'выведено по' ПравОтв) :-
bagof( Прав: если Условие то Цель с Сила, Правила),
% Все правила, относящиеся к цели
априори( Цель, Вер0),
% Априорная вероятность цели
модиф( Вер0, Правила, Трасса, Вер, ПравОтв).
% Модифицировать априорные вероятности
рассмотреть( Цель1 и
Цель2, Трасса,
( Цель1 и Цель2 : Вер было 'выведено из'
( Ответ1 и Ответ2) ) :-
!,
рассмотреть( Цель1, Трасса, Ответ1),
рассмотреть( Цель2, Трасса, Ответ2),
вероятность( Ответ1, В1),
вероятность( Ответ2, В2),
мин( В1, В2, Вер).
рассмотреть( Цель1
или Цель2, Трасса,
( Цель или Цель2:Вер) было 'выведено из'
( Ответ1 и Ответ2) ) :-
!,
рассмотреть( Цель1, Трасса, Ответ1),
рассмотреть( Цель2, Трасса, Ответ2),
вероятность( Ответ1, В1),
вероятность( Ответ2, В2),
макс( В1, В2, Вер).
рассмотреть( не
Цель, Трасса,
( не Цель:Вер) было 'выведено из' Ответ) :-
!,
рассмотреть( Цель, Трасса, Ответ),
вероятность( Ответ, В),
обратить( В, Вер).
рассмотреть( Цель,
Трасса, ( Цель: Вер) было сказано) :-
ответпольз( Цель, Трасса, Вер).
% Ответ, выведенный пользователем
% Отношение
%
% модиф( Вер0, Правила, Трасса, Вер, ПравОтв)
%
% Существует Цель с априорной вероятностью Вер0.
Правила имеют
% отношение к утверждению Цель; суммарное влияние
этих правил
% (точнее, их условных частей) на Вер0 приводит к
тому,
% что Вер0 заменяется на апостериорную
вероятность Вер;
% Трасса - список целей-предков и правил,
использовавшихся
% при выводе утверждения Цель;
% ПравОтв - результаты анализа условных частей
% правил из списка Правила.
модиф( Вер0, [ ],
Трасса, Вер0, [ ]).
% Нет правил - нет модификации
модиф( Вер0,
[ Прав : если Усл то Цель с Сила | Правила],
Трасса, Вер, [Прав из Ответ | ПравОтв] ):-
рассмотреть( Усл, [Цель по Прав | Трасса], Ответ),
% Условие из первого правила
априори( Усл, В0),
вероятность( Ответ, В),
импликация( В0, В, Сила, Вер0, Вер1),
% "Мягкая" импликация
модиф( Вер1, Правила, Трасса, Вер, ПравОтв).
Рис. 14. 16. Определение
степени правдоподобия гипотезы при помощи
распространения информации об оценке
уверенности по сети вывода.
Назад | Содержание | Вперёд